Posts

  • Feb 27, 2022

    The Meaning of ACID Consistency

    For backend/full-stack software engineers and system design interviews, I highly recommend “Designing Data-Intensive Applications: The Big Ideas Behind Reliable, Scalable, and Maintainable Systems” by Dr. Martin Kleppmann.

    Kleppmann Book Cover I want to share how this book explains ACID consistency. ACID is a set of properties intended to guarantee data validity after any transaction, which can sometimes be composed of multiple database operations. A transaction satisfies the ACID properties if it

    • completely fails, returning the database to its original state by discarding all writes, when any of its statements fail to complete (atomicity),
    • transitions the database from one valid state to another (consistency),
    • does not conflict with concurrent execution of other transactions (isolation), and
    • remains committed regardless of hardware faults, database crashes, etc. (durability).

    In my experience, when ACID consistency is explained, the focus is usually on defining integrity constraints in order to prevent database corruption (see https://en.wikipedia.org/wiki/ACID).

    However, an application’s notion of consistency may require enforcing constraints that the database cannot. So, at the end of the day, it is actually the application that is responsible for preserving consistency by defining its transactions correctly. For this reason, Dr. Kleppmann concludes that consistency is actually a property of the application, unlike atomicity, isolation, and durability, and that “the letter C doesn’t really belong in ACID” (page 225).

  • Nov 6, 2021

    Walking through the quicksort subroutine

    As discussed previously, quicksort uses the following subroutine, implemented in JavaScript, to rearrange the elements in an array.

    partition.test.js

    const expect = require('chai').expect;
const partition = require('./partition');

describe('partition', () => {
    it('rearranges `arr` from [46,50,99,32,49] to [46,32,49,50,99] and returns 2', () => {
        const arr = [46,50,99,32,49];
        const p = 0;
        const r = arr.length - 1;
        const actual_q = partition(arr,p,r);
        const expected_arr = [46,32,49,50,99];
        const expected_q = 2;
        expect(expected_arr).to.deep.equal(arr); // in-place sorting
        expect(expected_q).to.equal(actual_q)
    });
});

    partition.js

    module.exports = (arr, p, r) => {
    let i = p - 1;
    for (let j = p; j < r; j++) {
        if (arr[j] <= arr[r]) {
            i += 1;
            exchange(arr, i, j);
        }
    }
    const q = i + 1;
    exchange(arr, q, r);
    return q;
}

// helper function
const exchange = (arr, i, j) => {
    const temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

    Now, we will walk through what the subroutine does for the unit test above. Note that

    • p is used to set the initial values of i and j,
    • inside the loop, the values located at i (incremented before the exchange) and j are only exchanged if arr[j] is less than or equal to arr[r], as is the case when j = 0 and j = 3 in this example, and,
    • after the loop, the values located at q (set to i + 1) and r are exchanged.
    j = 3
    j = 3
    r
    r
    j
    j
    i
    i
    46
    46
    32
    32
    99
    99
    50
    50
    49
    49
    r
    r
    j
    j
    i
    i
    Exchange
    Exchange
    46
    46
    50
    50
    99
    99
    32
    32
    49
    49
    j
    j
    i
    i
    j = 0
    j = 0
    r
    r
    46
    46
    50
    50
    99
    99
    32
    32
    49
    49
    i,j
    i,j
    r
    r
    Exchange
    Exchange
    46
    46
    50
    50
    99
    99
    32
    32
    49
    49
    j = 1
    j = 1
    r
    r
    j
    j
    i
    i
    46
    46
    50
    50
    99
    99
    32
    32
    49
    49
    j = 2
    j = 2
    r
    r
    j
    j
    i
    i
    46
    46
    50
    50
    99
    99
    32
    32
    49
    49
    46
    46
    32
    32
    49
    49
    50
    50
    99
    99
    After Loop
    After Loop
    r
    r
    j
    j
    q = i+1
    q = i+1
    Exchange
    Exchange    Viewer does not support full SVG 1.1
  • Nov 3, 2021

    An important subroutine used by quicksort

    Quicksort is an in-place sorting algorithm that uses an important subroutine for partitioning. The following JavaScript code implements quicksort.

    const partition = require('./partition');

const quicksort = (arr, p, r) => {
    if (p < r) {
        const q = partition(arr, p, r);
        quicksort(arr, p, q - 1);
        quicksort(arr, q + 1, r);
    }
}

module.exports = quicksort;

    This algorithm uses the divide-and-conquer approach, which divides the original problem into multiple problems that are similar but smaller, conquers these sub-problems by solving them recursively, and then combines all the solutions to the sub-problems to create a solution to the original problem.

    Quicksort uses the partition subroutine to divide the original problem. It computes the index q and rearranges the array arr[p..r] such that all the values in the array with a smaller index than q, the arr[p..q-1] sub-array, are less than or equal to the value arr[q]. On the other hand, all the values that have an index greater than q, the arr[q+1..r] sub-array, are greater than arr[q]. Here is an implementation of this subroutine.

    partition.js

    module.exports = (arr, p, r) => {
    let i = p - 1;
    for (let j = p; j < r; j++) {
        if (arr[j] <= arr[r]) {
            i += 1;
            exchange(arr, i, j);
        }
    }
    exchange(arr, i + 1, r);
    return i + 1;
}

// helper function
const exchange = (arr, i, j) => {
    const temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

    After the division comes the conquest. So, the sub-arrays arr[p..q-1] and arr[q+1..r] are then sorted by recursive calls to quicksort. Since everything was done in place, the entire array arr[p..r] is sorted after these recursive calls and no additional work is needed to combine all the solutions to the sub-problems.

  • Oct 25, 2021

    Checking for Integer Divisibility Using Binary Search

    In a previous post, we proved that if $a = qd$ for integers $a, q, d$ such that $d \neq 0$, then $ \lvert a \rvert \geq \lvert q \rvert$. So, if we can find an integer $q$ in $[-a, a]$ such that $a = qd$, then we can say that $d$ divides $a$. The approach we used had a linear time complexity — some function of $2a + 1$ — because we naïvely checked each possible $q$ within that range.

    However, we can find $q$ much faster by using binary search. The following solution has a time complexity of $\mathcal{O}(\log a)$. It passes all the same test cases as our previous approach. Note that we are still not using the division operator here; in order to find mid, we use bit shifting.

    Some thought should be given to numeric overflow when $q$ and $d$ are large numbers.

    divides.test.js

    const expect = require('chai').expect;
const divides = require('./divides');

describe('divides', () => {
    // negatives
    it('returns true for -14 divides 28', () => {
        const expected = true;
        const actual = divides(-14, 28);
        expect(expected).to.equal(actual);
    });

    it('returns false for -14 divides 13', () => {
        const expected = false;
        const actual = divides(-14, 13);
        expect(expected).to.equal(actual);
    });

    it('returns true for 9 divides -18', () => {
        const expected = true;
        const actual = divides(9, -18);
        expect(expected).to.equal(actual);
    });

    it('returns false for 32 divides -2', () => {
        const expected = false;
        const actual = divides(32, -2);
        expect(expected).to.equal(actual);
    });

    it('returns true for -4 divides -56', () => {
        const expected = true;
        const actual = divides(-4, -56);
        expect(expected).to.equal(actual);
    });

    it('returns false for -5 divides -99', () => {
        const expected = false;
        const actual = divides(-5, -99);
        expect(expected).to.equal(actual);
    });

    // positives
    it('returns false for 15 divides 25', () => {
        const expected = false;
        const actual = divides(15, 25);
        expect(expected).to.equal(actual);
    });

    it('returns true for 9 divides 72', () => {
        const expected = true;
        const actual = divides(9, 72);
        expect(expected).to.equal(actual);
    });

    it('returns false for 27 divides 9', () => {
        const expected = false;
        const actual = divides(27, 9);
        expect(expected).to.equal(actual);
    });

    // zeroes
    it('returns true for 13 divides 0', () => {
        const expected = true;
        const actual = divides(13, 0);
        expect(expected).to.equal(actual);
    });

    it('returns false for 0 divides 42', () => {
        const expected = false;
        const actual = divides(0, 42);
        expect(expected).to.equal(actual);
    });

    it('returns false for 0 divides 0', () => {
        const expected = false;
        const actual = divides(0, 0);
        expect(expected).to.equal(actual);
    });

    // ones
    it('returns true for 1 divides 8', () => {
        const expected = true;
        const actual = divides(1, 8);
        expect(expected).to.equal(actual);
    });

    it('returns false for 13 divides 1', () => {
        const expected = false;
        const actual = divides(13, 1);
        expect(expected).to.equal(actual);
    });

    it('returns true for 1 divides 1', () => {
        const expected = true;
        const actual = divides(1, 1);
        expect(expected).to.equal(actual);
    });
});

    divides.js

    module.exports = (d, a) => {
    // some edge cases
    if (d == 0) {
        return false;
    }

    if (a == 0 || d == 1) {
        return true;
    }

    if (Math.abs(d) <= Math.abs(a)) {
        // carefully choosing our left and right indices cuts our
        // search range in half from [-a, a] to [-a, 0) or (0, a]
        let left;
        let right;

        if (a < 0) {
            if (d < 0) {
                left = 1;
                right = -a;
            } else {
                left = a;
                right = -1;
            }
        } else {
            if (d < 0) {
                left = -a;
                right = -1;
            } else {
                left = 1;
                right = a;
            }
        }

        // binary search
        while (left + 1 < right) {
            const mid = (left + right) >> 1;
            const prod = mid * d;
            if (a == prod) {
                return true;
            }

            if (d < 0) {
                if (a < prod) {
                    left = mid;
                } else {
                    right = mid;
                }
            } else {
                if (a < prod) {
                    right = mid;
                } else {
                    left = mid;
                }
            }
        }
    }
    return false;
}
  • Oct 24, 2021

    Custom Integer Division Function

    If we are not allowed to use the division operator in a programming language, how can we perform integer division? The following code uses repeated subtraction to achieve this; its time complexity is Big O of the quotient. One interesting tidbit: NaN is the only value in JavaScript that does not equal itself, so the last unit test had to be adjusted to account for this.

    integerDivision.test.js

    const expect = require('chai').expect;
const integerDivision = require('./integerDivision');

describe('integerDivision', () => {
    it('returns 0 for 2 divided by 7', () => {
        const expected = 3;
        const actual = integerDivision(7, 2);
        expect(expected).to.equal(actual);
    });

    it('returns 0 for -4 divided by 9', () => {
        const expected = 0;
        const actual = integerDivision(-4, 9);
        expect(expected).to.equal(actual);
    });

    it('returns 0 for 3 divided by -11', () => {
        const expected = 0;
        const actual = integerDivision(3, -11);
        expect(expected).to.equal(actual);
    });

    it('returns 0 for -19 divided by -21', () => {
        const expected = 0;
        const actual = integerDivision(-19, -21);
        expect(expected).to.equal(actual);
    });

    it('returns 4 for 44 divided by 10', () => {
        const expected = 4;
        const actual = integerDivision(44, 10);
        expect(expected).to.equal(actual);
    });

    it('returns -4 for -21 divided by 5', () => {
        const expected = -4;
        const actual = integerDivision(-21, 5);
        expect(expected).to.equal(actual);
    });

    it('returns -7 for 35 divided by -5', () => {
        const expected = -7;
        const actual = integerDivision(35, -5);
        expect(expected).to.equal(actual);
    });

    it('returns 3 for -23 divided by -6', () => {
        const expected = 3;
        const actual = integerDivision(-23, -6);
        expect(expected).to.equal(actual);
    });

    it('returns 1 for -1 divided by -1', () => {
        const expected = 1;
        const actual = integerDivision(-1, -1);
        expect(expected).to.equal(actual);
    });

    it('returns 1 for 1 divided by 1', () => {
        const expected = 1;
        const actual = integerDivision(1, 1);
        expect(expected).to.equal(actual);
    });

    it('returns -1 for 1 divided by -1', () => {
        const expected = -1;
        const actual = integerDivision(1, -1);
        expect(expected).to.equal(actual);
    });

    it('returns 0 for 0 divided by 13', () => {
        const expected = 0;
        const actual = integerDivision(0, 13);
        expect(expected).to.equal(actual);
    });

    it('returns -0 for 0 divided by -23', () => {
        const expected = -0;
        const actual = integerDivision(0, -23);
        expect(expected).to.equal(actual);
    });

    it('returns Infinity for 41 divided by 0', () => {
        const expected = Infinity;
        const actual = integerDivision(41, 0);
        expect(expected).to.equal(actual);
    });

    // NaN is the only value is javascript that does not equal itself
    it('returns NaN for "a" divided by 9', () => {
        const expected = NaN;
        const actual = integerDivision("a", 9);
        expect(isNaN(actual)).to.equal(true);
    });
});

    integerDivision.js

    module.exports = (a,b) => {
    // Return NaN if 'a' or 'b' are not numbers
    if (isNaN(a) || isNaN(b))
        return NaN;

    // Return Infinity like the JavaScript
    // division operator does when 'b' is 0
    if (b == 0)
        return Infinity

    // Use this bool to return a negative result
    // when 'a' or 'b' and not both are negative
    let negative = false;

    // If negative, replace 'a' with its absolute
    // value and toggle the 'negative' bool, then
    // do the same for 'b'
    if (a < 0) {
        a = a * -1;
        negative = !negative;
    }

    if (b < 0) {
        b = b * -1;
        negative = !negative;
    }

    // Count the number of time that 'b' goes into 'a'
    let count = 0;
    while (a >= b) {
        a = a - b;
        count++
    }
    return negative ? -count : count;
}
  • Oct 23, 2021

    Checking for Integer Divisibility

    Suppose that we are not allowed to use the division operator or remainder operator in a programming language such as JavaScript. With this constraint, how can we check whether or not an integer evenly divides another? Consider the following approach.

    Definition. Let $a$ and $d$ be integers. We say that $d$ divides $a$ if there exists an integer $q$ such that $a=qd$.

    Proposition. Let $a, q, d$ be integers such that $d \neq 0$. If $a = qd$, then $ \lvert a \rvert \geq \lvert q \rvert$.

    Proof. Since $ a=qd $ implies that $\lvert a \rvert = \lvert qd \rvert = \lvert q \rvert \cdot \lvert d \rvert \geq \lvert q \rvert $, then $\lvert a \rvert \geq \lvert q \rvert$. Thus, if $a = qd$, then $\lvert a \rvert \geq \lvert q \rvert$. $\blacksquare$

    So, in order to check whether $d$ divides $a$, a computer program would just have to search for an integer $q$ between $-a$ and $a$ (inclusive) such that $a = qd$. The following approach has linear time complexity, a function of $a$; I would describe it as being naïve or brute force.

    Some thought should be given to numeric overflow when $q$ and $d$ are large numbers.

    divides.test.js

    const expect = require('chai').expect;
const divides = require('./divides');

describe('divides', () => {
    // negatives
    it('returns true for -14 divides 28', () => {
        const expected = true;
        const actual = divides(-14, 28);
        expect(expected).to.equal(actual);
    });

    it('returns false for -14 divides 13', () => {
        const expected = false;
        const actual = divides(-14, 13);
        expect(expected).to.equal(actual);
    });

    it('returns true for 9 divides -18', () => {
        const expected = true;
        const actual = divides(9, -18);
        expect(expected).to.equal(actual);
    });

    it('returns false for 32 divides -2', () => {
        const expected = false;
        const actual = divides(32, -2);
        expect(expected).to.equal(actual);
    });

    it('returns true for -4 divides -56', () => {
        const expected = true;
        const actual = divides(-4, -56);
        expect(expected).to.equal(actual);
    });

    it('returns false for -5 divides -99', () => {
        const expected = false;
        const actual = divides(-5, -99);
        expect(expected).to.equal(actual);
    });

    // positives
    it('returns false for 15 divides 25', () => {
        const expected = false;
        const actual = divides(15, 25);
        expect(expected).to.equal(actual);
    });

    it('returns true for 9 divides 72', () => {
        const expected = true;
        const actual = divides(9, 72);
        expect(expected).to.equal(actual);
    });

    it('returns false for 27 divides 9', () => {
        const expected = false;
        const actual = divides(27, 9);
        expect(expected).to.equal(actual);
    });

    // zeroes
    it('returns true for 13 divides 0', () => {
        const expected = true;
        const actual = divides(13, 0);
        expect(expected).to.equal(actual);
    });

    it('returns false for 0 divides 42', () => {
        const expected = false;
        const actual = divides(0, 42);
        expect(expected).to.equal(actual);
    });

    it('returns false for 0 divides 0', () => {
        const expected = false;
        const actual = divides(0, 0);
        expect(expected).to.equal(actual);
    });

    // ones
    it('returns true for 1 divides 8', () => {
        const expected = true;
        const actual = divides(1, 8);
        expect(expected).to.equal(actual);
    });

    it('returns false for 13 divides 1', () => {
        const expected = false;
        const actual = divides(13, 1);
        expect(expected).to.equal(actual);
    });

    it('returns true for 1 divides 1', () => {
        const expected = true;
        const actual = divides(1, 1);
        expect(expected).to.equal(actual);
    });
});

    divides.js

    module.exports = (d, a) => {
    // some edge cases
    if (d == 0) {
        return false;
    }

    if (a == 0 || d == 1) {
        return true;
    }

    if (Math.abs(d) <= Math.abs(a)) {
        let start = -a;
        let end = a;
        if (a < 0) {
            start = a;
            end = -a;
        }
        for (let q = start; q <= end; q++)
            if (a === q * d)
                return true;
    }
    return false;
}
  • Oct 23, 2021

    Node.js TDD Project

    According to Wikipedia, test-driven development (TDD) is a software development process that converts software requirements into test cases before the software is actually developed. The steps of the TDD cycle are as follows:

    1. Add a test (the new test should fail)
    2. Write the simplest code that makes the new test pass (YAGNI)
    3. Refactor the code

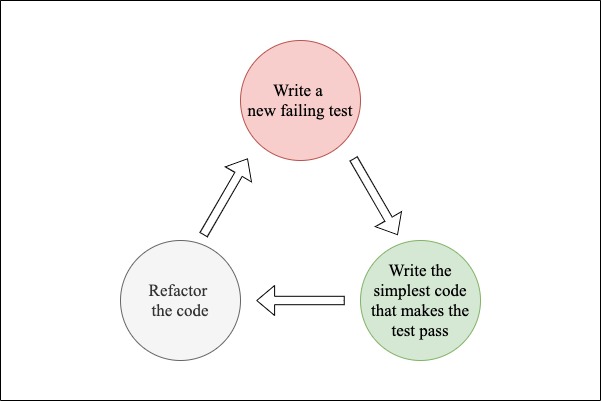
    TDD Cycle

    So, in order to set up a Node.js project for TDD, we need a way to run unit tests on the code that will be developed for it. There are two popular tools for doing this: Mocha is a popular JavaScript test framework and Chai is an assertion library that can be nicely paired with it.

    We can get started by launching a bash shell and running the following commands to initialize such a project.

    mkdir tdd-project
cd tdd-project
npm init -y
npm install --save-dev mocha
npm install --save-dev chai

    The tdd-project directory should now have a new file called package.json which contains the following:

    {
  "name": "tdd-project",
  "version": "1.0.0",
  "description": "",
  "main": "index.js",
  "scripts": {
    "test": "echo \"Error: no test specified\" && exit 1"
  },
  "keywords": [],
  "author": "",
  "license": "ISC",
  "devDependencies": {
    "chai": "^4.3.4",
    "mocha": "^9.1.3"
  }
}

    Now all we have to do is modify the scripts property in this file. We could simply make the test script run the mocha command. However, mocha by default only finds test files with extensions .js, .mjs, and .cjs in a directory named test. On the other hand, the following script finds all test files ending with .test.js in all directories except node_modules.

    {
  "name": "tdd-project",
  "version": "1.0.0",
  "description": "",
  "main": "index.js",
  "scripts": {
    "test": "mocha \"./{,!(node_modules)/**/}*.test.js\""
  },
  "keywords": [],
  "author": "",
  "license": "ISC",
  "devDependencies": {
    "chai": "^4.3.4",
    "mocha": "^9.1.3"
  }
}

    After adding the test script, we can then run all tests by calling npm test in the project directory. To get started with writing test files, we create a new file somewhere within the project (not in the node_modules directory of course) named sample.test.js. Then we add the following contents:

    const expect = require('chai').expect;

describe('sample', () => {
    it('fails this test', () => {
        expect(true).to.equal(false);
    });
});

    Running npm test should now return the following:

    
> tdd-project@1.0.0 test
> mocha "./{,!(node_modules)/**/}*.test.js"



  sample
    1) fails this test


  0 passing (2ms)
  1 failing

  1) sample
       fails this test:

      AssertionError: expected true to equal false
      + expected - actual

      -true
      +false

      at Context.<anonymous> (sample.test.js:5:19)
      at processImmediate (node:internal/timers:464:21)

    Congratulations on writing your first failing test! I have placed all the code in this post in a Github repository for your convenience: https://github.com/miguelamezola/tdd-project.git

  • Sep 18, 2021

    Numbers Everyone Should Know

    These performance numbers were put out by Jeff Dean more than 10 years ago. Since hardware has improved, they are now outdated. However, they still give us some idea of how the operations compare to one another. Simon Eskildsen has collected updated numbers in https://github.com/sirupsen/napkin-math.

    Operation Latency (ns)
    L1 cache reference 0.5
    Branch mispredict 5
    L2 cache reference 7
    Mutex lock/unlock 25
    Main memory reference 100
    Compress 1K w/cheap compression algorithm 3,000
    Send 2K bytes over 1 Gbps network 20,000
    Read 1 MB sequentially from memory 250,000
    Round trip within same datacenter 500,000
    Disk seek 10,000,000
    Read 1 MB sequentially from disk 20,000,000
    Send packet CA->Netherlands->CA 150,000,000
  • Aug 29, 2021

    Python defaultdict collection

    In python, defaultdict and dict are almost the same except that the former never raises a KeyError. Instead, it provides a default value for the key that does not exist. In the code below, seen is a defaultdict that has list[int] as its default value.

    from typing import List
from collections import defaultdict 

def two_sum(nums: List[int], target: int) -> List[int]:
    seen = defaultdict(list[int])
    for j in range(len(nums)):
        complement = target - nums[j]
        if complement in seen:
            return [seen[complement][0],j]
        seen[nums[j]].append(j)
    return []

    On the other hand, using dict would look something like this.

    from typing import List

def two_sum(nums: List[int], target: int) -> List[int]:
    seen = dict()
    for j in range(len(nums)):
        complement = target - nums[j]
        if complement in seen:
            return [seen[complement][0], j]
        if nums[j] in seen:
            seen[nums[j]].append(j)
        else:
            seen[nums[j]] = [j] 
    return []

    I like the first implementation better for its conciseness and human readability.

  • Aug 6, 2021

    Multics Simulator

    Multics was a mainframe timesharing operating system that began in 1965 and was used until 2000. Today I found out that there’s a simulator that can create a Multics machine and that it can even run on a Raspberry Pi! https://multicians.org/

  • Jul 5, 2021

    Acceptance test studio project

    I really like Cucumber, a single tool for automated tests and living documentation, using executable specifications written in plain text. Since I’m searching for ways to enhance my portfolio, I think it would be fun to make an application that can edit and run these specifications from a web browser.

  • Jul 4, 2021

    A new focus on personal projects

    I really need to focus on completing personal projects. My portfolio has always needed improvement and I have just been pushing it off. I think I’ll start scheduling time to work on this every week and discipline my self to follow the plan.

  • Jun 4, 2021

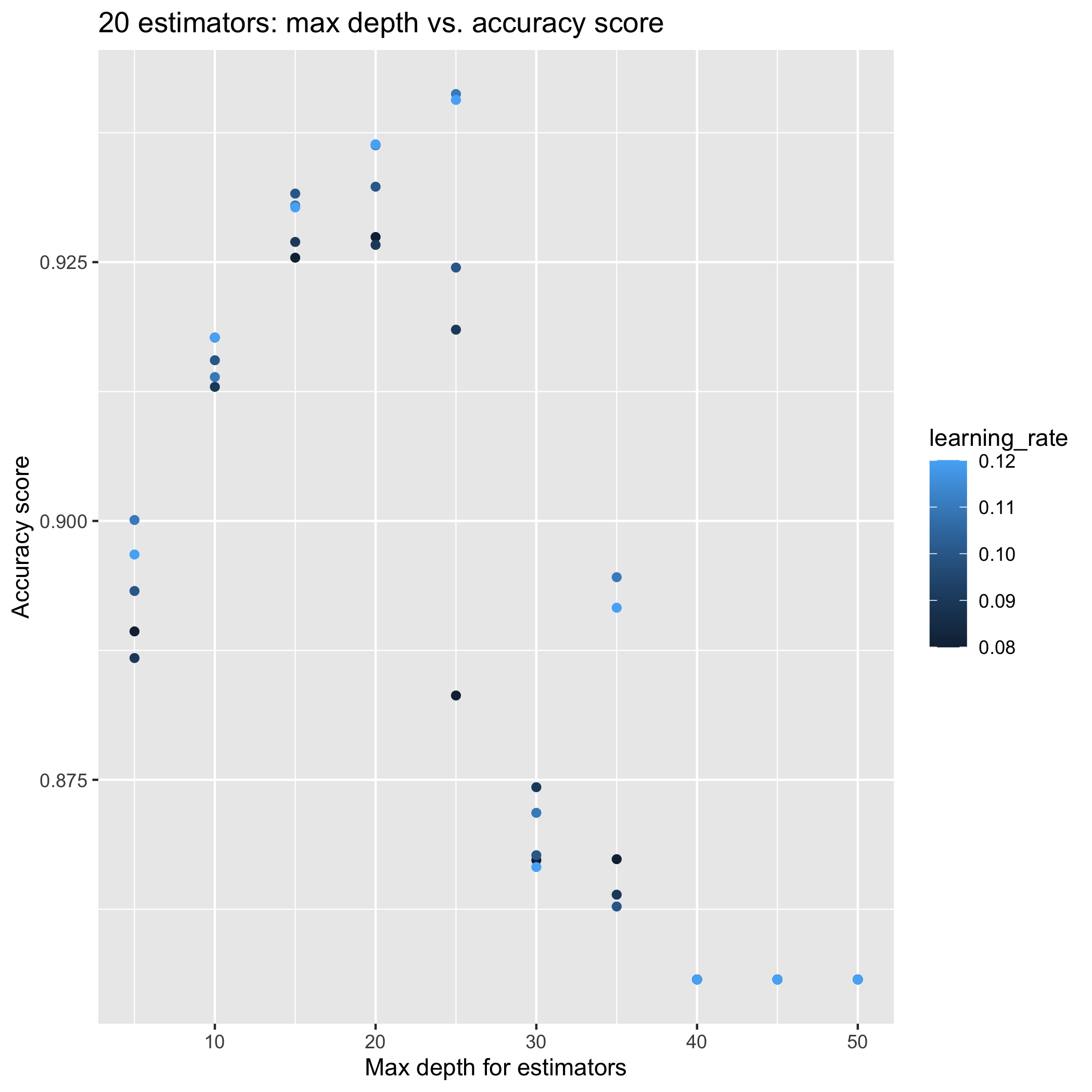
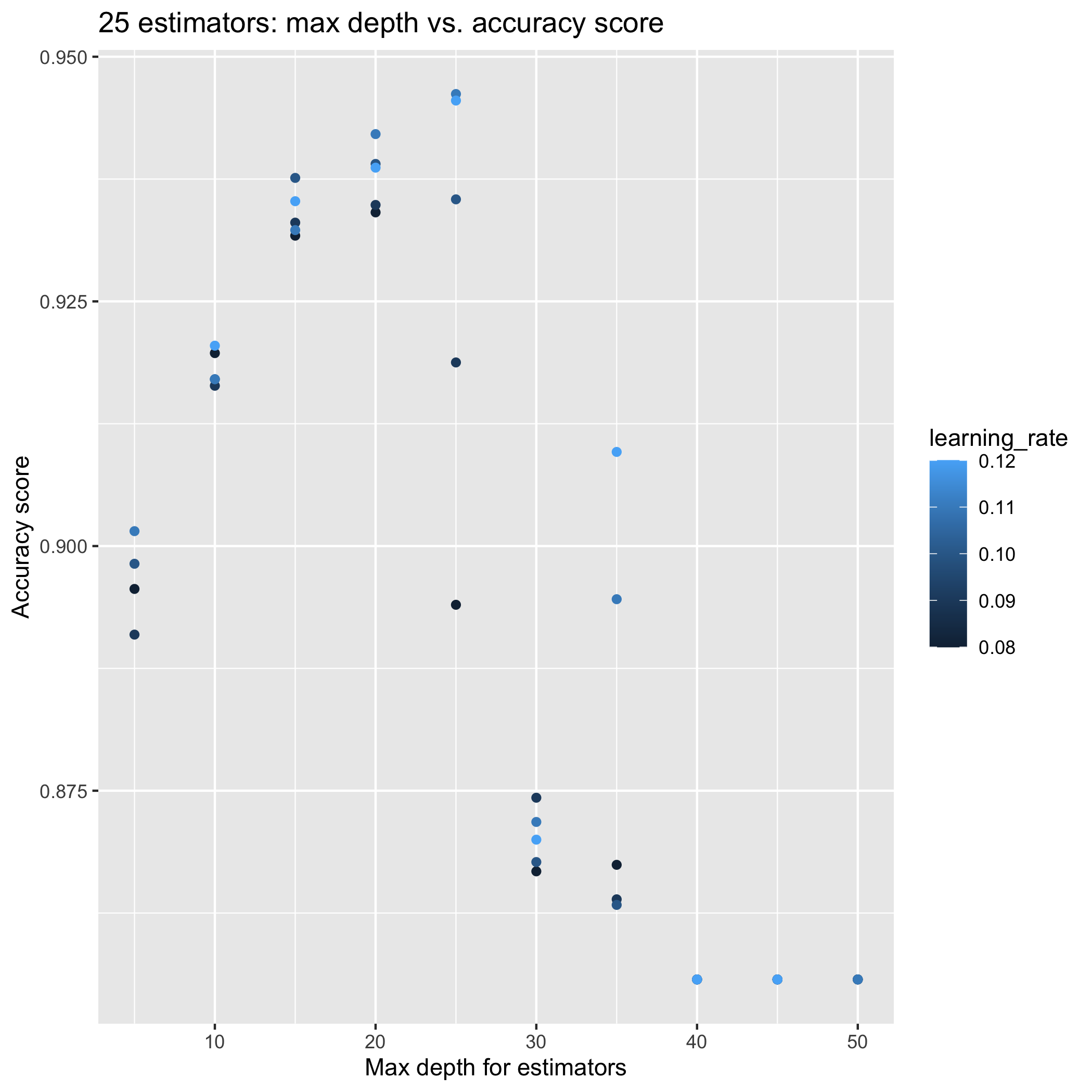
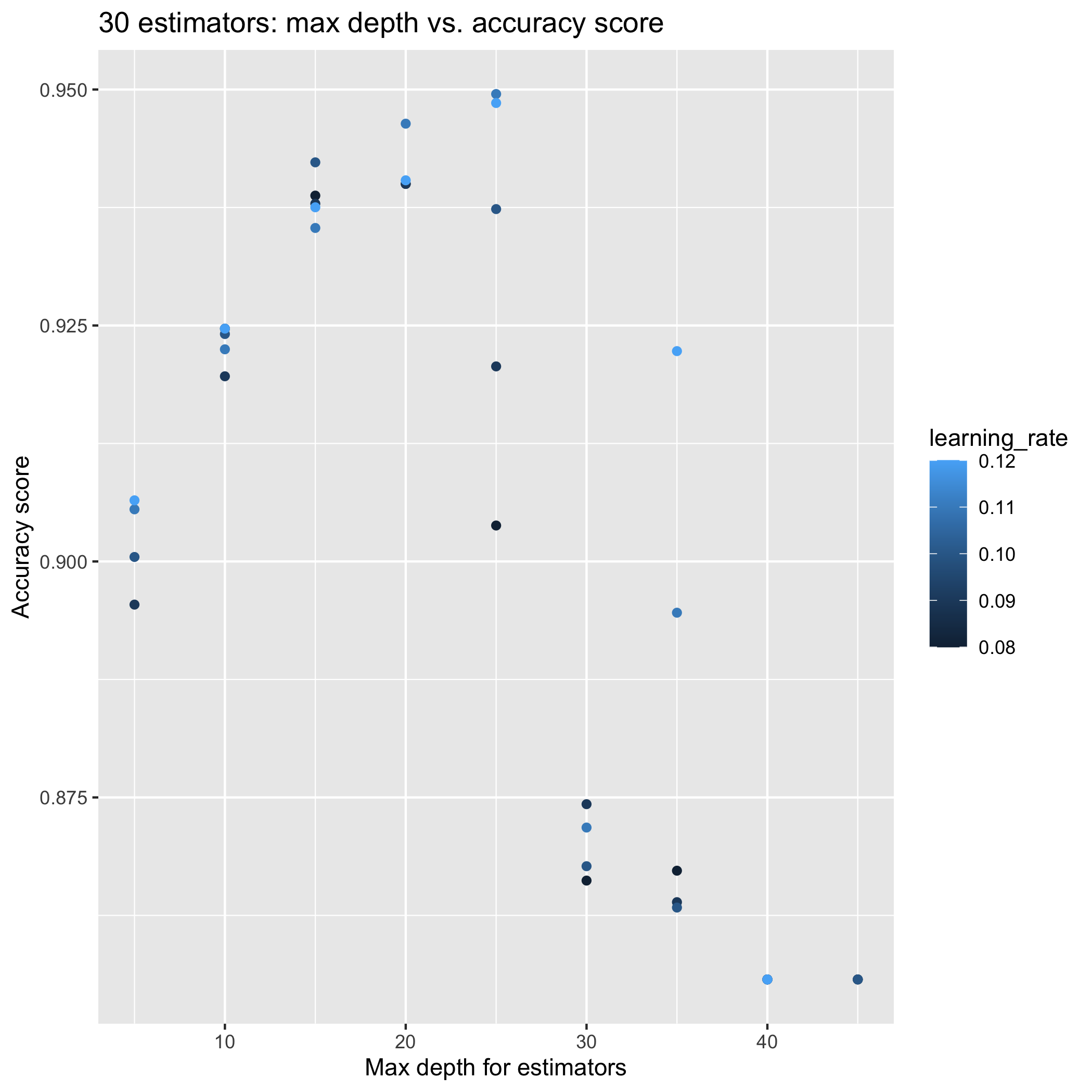
    AdaBoost model near 0.95 training accuracy

    Tuning the number of estimators, learning rate, and max depth for the base estimator tree has improved the model. Now, I need to investigate whether or not that the model is over-fitting the training data. New submission to the Kaggle competition is in the works.

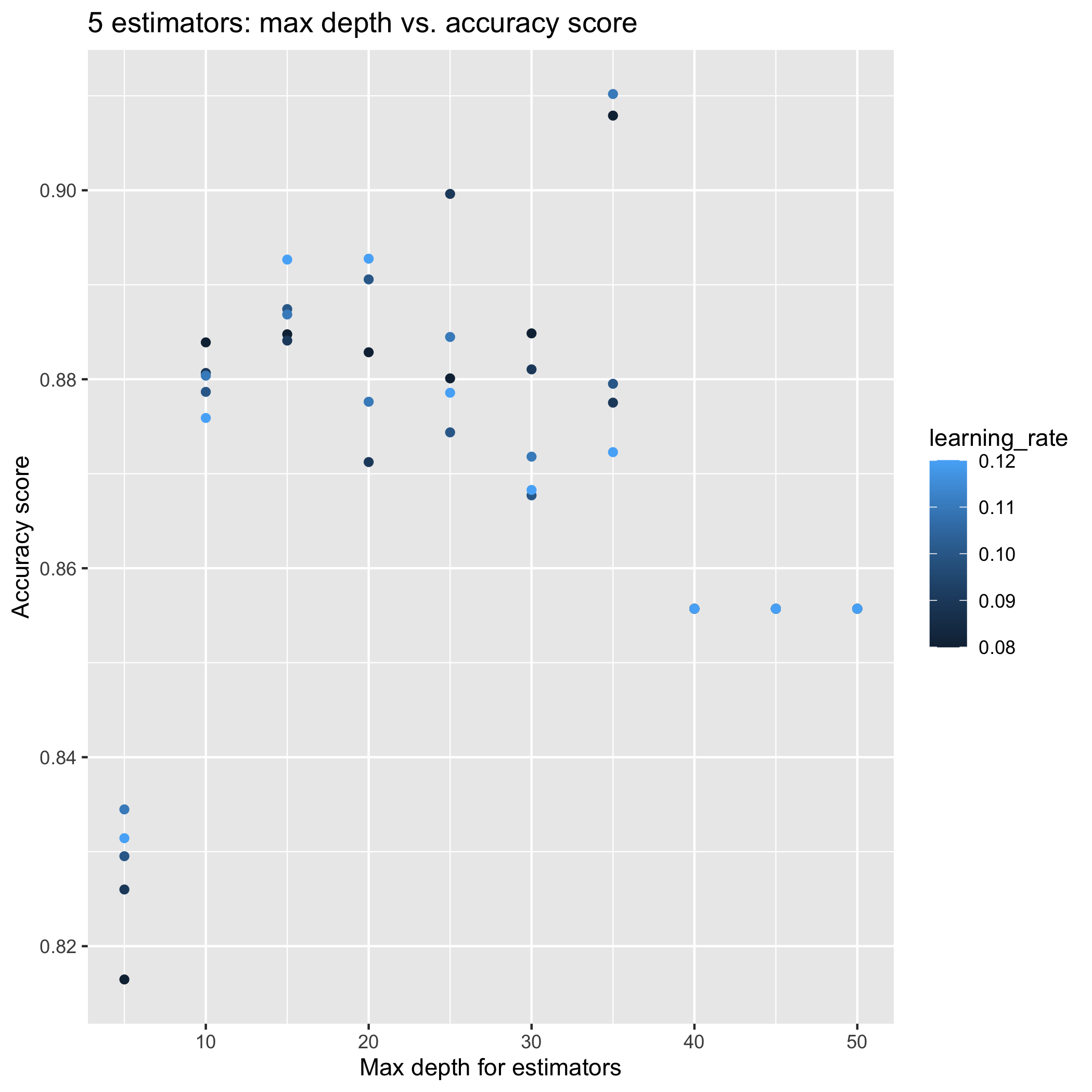
    Accuracy results for n_estimators = 5

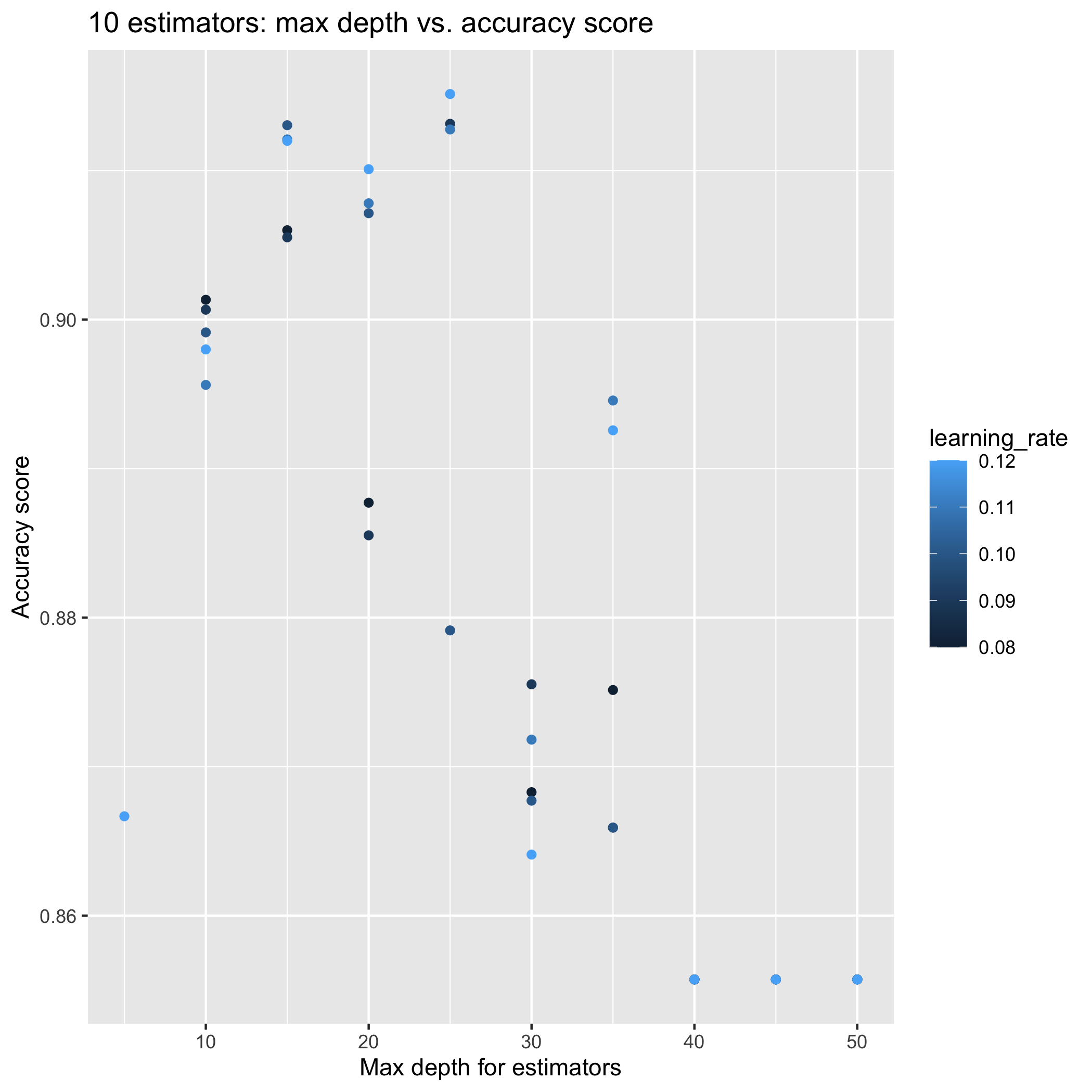
    Accuracy results for n_estimators = 10

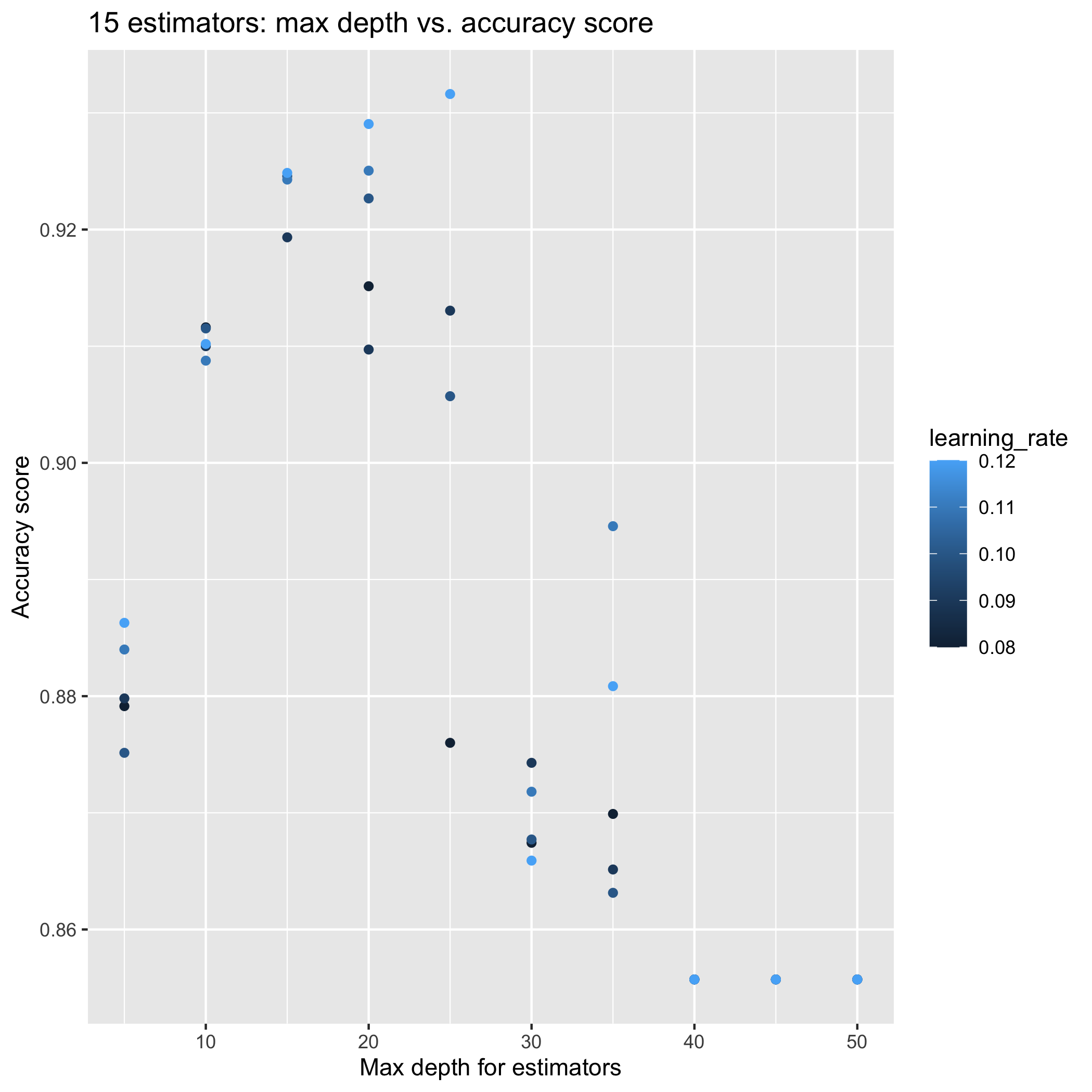
    Accuracy results for n_estimators = 15

    Accuracy results for n_estimators = 20

    Accuracy results for n_estimators = 25

    Accuracy results for n_estimators = 30

  • Jun 3, 2021

    Tweaking AdaBoost hyperparameters

    I have to admit, yesterday I had already given up on using AdaBoost on the MNIST data set. But I had only been adjusting its n_estimators and learning_rate hyperparameters. So, I decided to try using a large number of estimators (200 - 1000), tweaking the learning rate (0.2,0.25,0.3,0.35), and changing the classification tree max depth for the base estimator (1,2,3).

    
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X_train, X_val, y_train, y_val = train_test_split(X, y)

n_trees = [200, 400, 600, 800, 1000]
depths = [1,2,3]
rates = [0.2,0.25,0.3,0.35]

for n_estimators in n_trees:
    ada_clf.n_estimators = n_estimators;
    
    for depth in depths:
        ada_clf.base_estimator =  tree(random_state=619,max_depth=depth)

        for learning_rate in rates:
            ada_clf.learning_rate = learning_rate
            
            ada_clf.fit(X_train, y_train)
            y_pred = ada_clf.predict(X_val)
            accuracy = accuracy_score(y_val, y_pred)
            print(n_estimators,depth,learning_rate,accuracy)

    The results are promising: this model blew past the training accuracy scores attained by the CART classification tree I used a few days ago on this data set. The best model has an accuracy of 0.896 (rounded to the nearest thousandth); using 800 estimators, a max depth of 3, and a 0.20 learning rate.

  • Jun 2, 2021

    AdaBoost approach to MNIST

    Three days ago, I trained a CART classification tree model on the MNIST data set. I submitted its predictions to the Digit Recognizer competition on Kaggle, which uses this data set. The submission received an accuracy score of 0.86346.

    So, I was expecting for this AdaBoost model that I’m training today to perform better; its base algorithm is also a classification tree. Surprisingly, it hasn’t received an accuracy score greater than 0.81 on the training set. I think this indicates that tree-based algorithms do not perform well on this data set.

    AdaBoost Notebook Screenshot

  • Jun 1, 2021

    Cricket chirping correlated to ambient temperature

    I never knew that crickets chirp faster as their ambient temperature rises but it’s true! This could make for an awesome elementary school science project; i.e. the student can collect cricket data and then use a machine learning algorithm to predict the temperature given a chirp rate or vice versa.

  • May 31, 2021

    My first Kaggle competitions

    Over the weekend, I joined two popular knowledge competitions on Kaggle, Titanic - Machine Learning from Disaster and Digit Recognizer.

    I was very familiar with the first one, since I had implemented the CART algorithm in college and used this competition’s dataset to compare my implementation’s performance with that of scikit-learn Decision Trees. The second competition caught my eye because of its use of the famous MNIST dataset.

    I’m really excited about the Jupyter Notebooks environment offered by Kaggle. Here are my notebooks for these competitions: